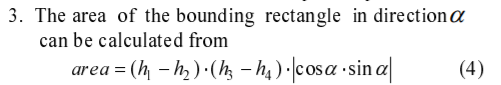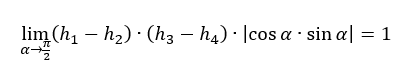- AppSheet
- AppSheet Forum
- AppSheet Q&A
- Plot land size (acres, sq feet)
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Has anyone successfully done anything like this? I’m about to give it a try but wanted to check first.
Capture land square footage or acreage using 3-4 data points collected from an app.
Ex.
4 fields of type LatLong
Collect 3-4 data points by walking to 4 corners of your yard, then click “calculate”.
The output should be something like … 1.08 acres or 20,000 SQ FT.
- Labels:
-
UX
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have sent the device location to web services to retrieve other data, for weather, Air Quality Index, lookup zip code, etc. I’m sure this could be done if you find the right service to integrate.
Sounds like it would be a very useful tool. I have a few existing apps that could benefit from this. I’d be glad to help with the integration.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have looked into doing this for some of my applications. Its definitely doable, even without a third party service… However, the success is dependent upon inputting the points in a sequential/logical order, as reordering points in AS is cumbersome / unintuitive.
If you limit yourself to 4 points (quadrilaterals), then you can simply average opposite ends and multiply them to get an approximate area. This method can be somewhat inaccurate, particularly with larger or very irregular areas… but in the case of an acre plot of land, the larger source of error will likely be from the accuracy and precision of your devices GPS.
In any case, you could get a quick area estimate with AppSheet, but you wont be replacing legal survey.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
GreenFlux - you can email me at MatthewDavid122@gmail for more info
thanks guys, great feedback.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@Matthew_Brown
Unless you can’t ensure that the points are taken in strict order/direction (i.e. clockwise or counter-clockwise direction), you won’t be able to get an accurate calculation even with a 3rd party service. Provided you can maintain that data collection order, than it’s a very easy match calculation to do even without using a 3rd party service.
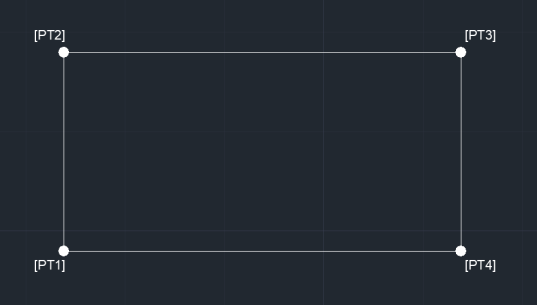
Assume 4 points as [PT1] to [PT4] and points taken in clockwise direction:
SQ FT CALCULATION
IFS(
DISTANCE([PT2],[PT1]) = DISTANCE([PT4],[PT3]),
IFS(
DISTANCE([PT3],[PT2]) < DISTANCE([PT4],[PT1]),
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT2],[PT1]) * (DISTANCE([PT4],[PT1]) - DISTANCE([PT3],[PT2]))) / 2) * 10763910.0000,
DISTANCE([PT3],[PT2]) > DISTANCE([PT4],[PT1]),
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT2],[PT1]) * (DISTANCE([PT3],[PT2]) - DISTANCE([PT4],[PT1]))) / 2) * 10763910.0000,
TRUE,
DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2]) * 10763910.0000
),
DISTANCE([PT2],[PT1]) > DISTANCE([PT4],[PT3]),
((DISTANCE([PT4],[PT3]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT3],[PT2]) * (DISTANCE([PT2],[PT1]) - DISTANCE([PT4],[PT3]))) / 2) * 10763910.0000,
TRUE,
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT3],[PT2]) * (DISTANCE([PT4],[PT3]) - DISTANCE([PT2],[PT1]))) / 2) * 10763910.0000
)
ACRES CALCULATION
IFS(
DISTANCE([PT2],[PT1]) = DISTANCE([PT4],[PT3]),
IFS(
DISTANCE([PT3],[PT2]) < DISTANCE([PT4],[PT1]),
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT2],[PT1]) * (DISTANCE([PT4],[PT1]) - DISTANCE([PT3],[PT2]))) / 2) * 247.1054,
DISTANCE([PT3],[PT2]) > DISTANCE([PT4],[PT1]),
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT2],[PT1]) * (DISTANCE([PT3],[PT2]) - DISTANCE([PT4],[PT1]))) / 2) * 247.1054,
TRUE,
DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2]) * 247.1054
),
DISTANCE([PT2],[PT1]) > DISTANCE([PT4],[PT3]),
((DISTANCE([PT4],[PT3]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT3],[PT2]) * (DISTANCE([PT2],[PT1]) - DISTANCE([PT4],[PT3]))) / 2) * 247.1054,
TRUE,
((DISTANCE([PT2],[PT1]) * DISTANCE([PT3],[PT2])) + (DISTANCE([PT3],[PT2]) * (DISTANCE([PT4],[PT3]) - DISTANCE([PT2],[PT1]))) / 2) * 247.1054
)
Of course this approach disregards the area to be a parallelogram shape rather than a perfect rectangle. However, if you consider Martin’s Law of Skewness, the area of a parallelogram (a rectangle which is shewed with an angle of alpha), the area can be interpreted as:
and provided the Skewness angle of the both opposite sides are equal than the area of that parallelogram is same than the perfect rectangle as the trigonometric limit approaches to 1
The latter case; provided the Skewness angle of the opposite sides are not equal than (which we call Obstructed Polygon) you will need an Eigen Vector to correct the vector calculation of the so called area, which will need a GPS Total Station and I’m afraid in this case even a 3rd party service can’t help you for that calculation.
Far more important, may be remind you that, the precision/accuracy of any GPS calculation strongly relies on the accuracy of the GPS accelerometer of the mobile device where it should be perfectly and appropriately calibrated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@Matthew_Brown, will @LeventK’s method work for you? I was thinking of something more flexible, with any number of points to make a polygon, and in any capture order.
I found this site, which uses a URL scheme that should be easy to integrate with AppSheet LatLong values.
www.mapdevelopers.com
This method easily supports more than 4 points. And I think you can get around the need to capture points in a certain order, if each point is saved in a new row in a related table. Then you could add a column for Order, and re-order the points prior to constructing the URL.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@GreenFlux
I’m a Construction Director in essence and we do a lot of topographic surveys on site. In general we only give the WCS benchmark coordinates to the surveyors and the plot’s map. The surveyors bind the GPS total station to that polygon point only once and it’s totally their choice to pick-up measuring points according how much the site have ease of access. So there is no way to know in what order they might have picked-up the points and in fact in terms of topography it’s totally irrelevant because at the end of the day, they import the coordinates to their AGIS software and draw the boundary poly-lines as per the map they have and the job is done.
So I believe here @Matthew_Brown does not have any chance to know in which order the guys pick the points unless and explicitly they are instructed to do so. Provided -/+ 15-20% errata is not important for the work he wants to accomplish, there is no big deal. However, on the contrary, provided he wants a good accuracy (i.e. -/+ 3-5%) than believe me this is not a good method in many ways. In our current construction site which have a 25M sq.ft. land, we are using TOPCON GPS Total Station which is far away number 1 instrument and it’s errata is around -/+ 1-2%. And this device is machine calibrated every 3 months ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have simplified my expression, because of the nature of the coordination, the evaluation of:
DISTANCE([PT1],[PT2]) = DISTANCE([PT3],[PT4])
does not make sense as it’s not so possible to maintain that equality
(((DISTANCE([PT1],[PT2]) + DISTANCE([PT3],[PT4])) / 2) * DISTANCE([PT2],[PT3])) * 10763910.0000
OR
(((DISTANCE([PT1],[PT2]) + DISTANCE([PT3],[PT4])) / 2) * DISTANCE([PT2],[PT3])) * 247.1054
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In general we’ve seen pretty poor GPS accuracy from the API that AppSheet uses to calculate the coordinates. For example, in the image below all of the points are clustered around one side of the rectangle; green edits show where the other side of the rectangle should be.
Has anyone had better accuracy on the GPS points? No use on plugging these points into another service for land area if the accuracy is so poor.
-
Account
1,676 -
App Management
3,097 -
AppSheet
1 -
Automation
10,318 -
Bug
981 -
Data
9,675 -
Errors
5,731 -
Expressions
11,776 -
General Miscellaneous
1 -
Google Cloud Deploy
1 -
image and text
1 -
Integrations
1,607 -
Intelligence
578 -
Introductions
85 -
Other
2,901 -
Photos
1 -
Resources
537 -
Security
827 -
Templates
1,307 -
Users
1,558 -
UX
9,109
- « Previous
- Next »
| User | Count |
|---|---|
| 39 | |
| 29 | |
| 23 | |
| 23 | |
| 13 |

 Twitter
Twitter